Pythagoras' Rule

Pythagoras' Theorem (in words):
The square of the hypotenuse is equal to the sum of the squares of the other two sides.
Pythagoras' Rule (in symbols):
To find the hypotenuse c2 = a2 + b2
To find another side a2 = c2 – b2
c is always the hypotenuse.
Remember to find the square root in the last step.
Did You Know That...?

Pythagoras was a 6th century BC Greek philosopher, mathematician and founder of a religious cult named the Pythagoreans who believed in reincarnation. He played an active role in the politics, but had to flee from his home when his teachings became unpopular. Now, he is best known for his Pythagorean Theorem and Pythagorean Triples.
Question - Pythagoras' Rule with Squares on Three Sides
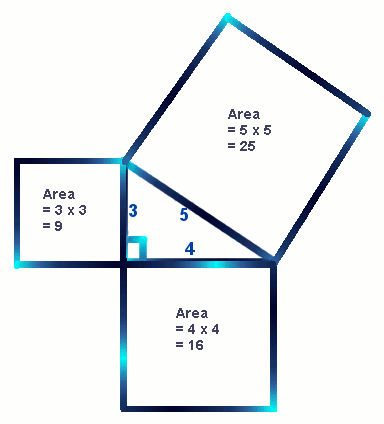
Here is a right triangle with sides of 3, 4 and 5.
Using areas of squares, you can see that 32 + 42 = 52
Does it work with other numbers?
Maths Fun - Pythagoras' Rule with Semi-Circles on Three Sides

Does Pythagoras' Rule work with the areas of shapes other than squares? Calculate the areas of these semi-circles. What do you notice?
Example One - Finding the Hypotenuse

Find the hypotenuse of a right-angled triangle whose perpendicular sides are 5 and 12.
Answer:
a = 5
b = 12
c2 = a2 + b2
= 52 + 122
= 25 + 144
= 169
c = √169 (Remember to find the square root.)
= 13
Example Two - Finding the Hypotenuse

A carpenter building these stairs must calculate the length of the supporting timber beam underneath. The vertical and horizontal lengths are 200 cm and 210 cm.
Answer:
a = 200
b = 210
c2 = a2 + b2
= 2002 + 2102
= 40000 + 44100
= 84100
c = √84100 (Remember to find the square root.)
= 290 cm
Example Three - Finding a Side

In a right-angled triangle, the hypotenuse is 10. One side is 8. What's the length of the other side?
Answer:
c = 10
b = 8
a2 = c2 – b2
= 102 – 82
= 100 – 64
= 36
a = √36
= 6
Example Four - Finding a Side

A skydiver, instead of falling directly downward, is blown by the wind as shown in the diagram. In the right triangle, the hypotenuse is 26 metres and the vertical fall is 24 metres. What is the horizontal distance by which she will miss her landing target?
Answer:
c = 26 metres
b = 24 metres
a2 = c2 – b2
= 262 – 242
= 676 – 576
= 100
a = √100
= 10 metres off target
Questions
Q1. What is the hypotenuse of a right triangle whose perpendicular sides are 26 and 168?
Q2. Find the other side of a right triangle if the hypotenuse is 205 and one side is 45.
Answers
A1. 170
A2. 200
Maths Fun - Area of Regular Hexagon
A regular hexagon has 6 equal sides. It can be divided into 2 equilateral triangles joined at the centre of the hexagon. If each side of the hexagon has a length of 1 unit, prove that the area of the hexagon is approximately 2.6 times the square of the side length.

| 
| 
|