Standard Deviation

The Variance and the Standard Deviation are measures of spread of the data indicating how far the data is away from the normal (mean).

When data such as people's heights, weights, intelligence, school test marks and so forth are graphed, they tend to create a "bell-shaped curve" or normal distribution curve.

Mathematical Symbols:

• Mean μ
• Variance σ ²
• Standard Deviation σ

Normal Distribution Graph:

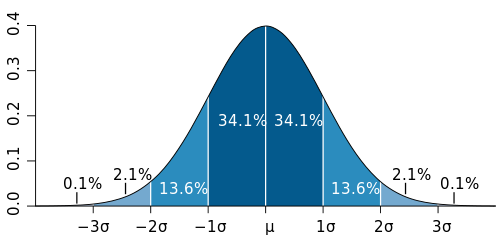
A Normal Distribution curve with sufficient data has the following features:

• The Mean is in the middle.
• The Highest Score is the Mean plus 3 Standard Deviations.
• The Lowest Score is the Mean minus 3 Standard Deviations.

---

Finding the Standard Deviation of a Population

• Calculate the Mean of all the data (by adding up all the numbers and dividing by how many numbers there are).
• For each data number, subtract it from the Mean.
• Square this difference. This is called the Squared Difference.
• Find the Mean of the Squared Differences. This is called the Variance.
• Find the Square Root of the Variance. This is called the Standard Deviation.

---

Example One - Intelligence Quotient (IQ)

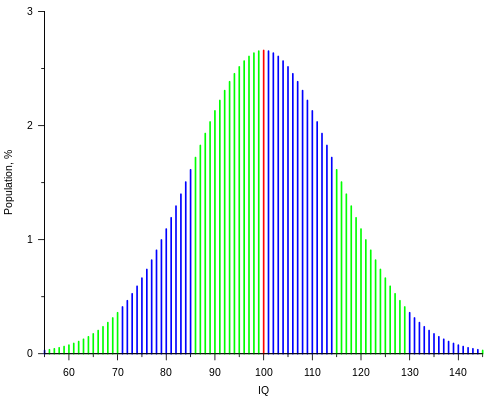
In most IQ tests, the "average" or Mean IQ is about 100 and the Standard Deviation is about 15. The vast majority of people have IQs between 70 and 130. However, famous physicists Albert Einstein and Stephen Hawking (in the photographs above) are thought to have IQs of about 145 (which is equal to the Mean plus 3 Standard Deviations). Refer to the instructions above to calculate the mean, the variance and the standard deviation of the IQ data of the following fictitious people listed in this table.

PERSON	IQ
Al	76
Bert	80
Cuc	89
David	96
Eng	100
Fran	102
Gianni	106
Helena	108
Ines	122
Jack	130

Answer:

PERSON	IQ	IQ DIFFERENCE FROM THE MEAN	SQUARE OF THE IQ DIFFERENCE FROM THE MEAN
Al	76	– 24.9	620.01
Bert	80	– 20.9	436.81
Cuc	89	– 11.9	141.61
David	96	– 4.9	24.01
Eng	100	– 0.9	0.81
Fran	102	+ 1.1	1.21
Gianni	106	+ 5.1	26.01
Helena	108	+ 7.1	50.41
Ines	122	+ 21.1	445.21
Jack	130	+ 29.1	846.81
	MEAN IQ = 100.9		MEAN OF SQUARED DIFFERENCES = 259.29

Mean = 100.9
Variance = 259.29

Standard Deviation	= square root of variance
	= √ 259.29 = 16.1

---

Example Two - World's Tallest Structures

STRUCTURE	HEIGHT IN METRES
Great Pyramid of Giza	139
Eiffel Tower	300
Empire State	381
Petronas Towers	452
Taipei 101	509
World Trade Centre	526
CN Tower	553
KVLY-TV Mast	629
Warsaw Radio Mast	646
Burj Khalifa	830

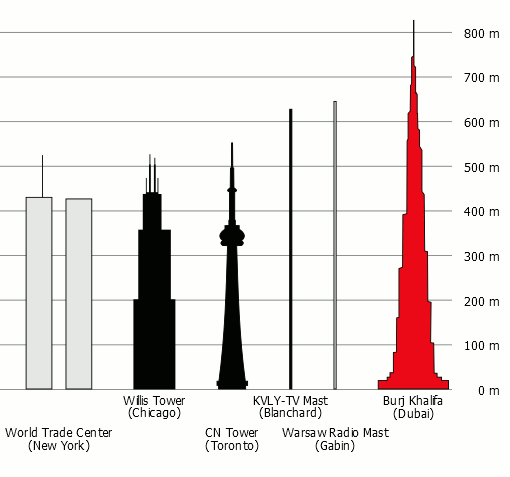
The graph and the table show the heights of ten of the world's tallest structures. Draw a table and then calculate the:
(a) mean
(b) variance
(c) standard deviation.

Answer:

STRUCTURE	HEIGHT IN METRES	HEIGHT DIFFERENCE FROM THE MEAN	SQUARE OF THE HEIGHT DIFFERENCE FROM THE MEAN
Great Pyramid of Giza	139	– 357.5	127 806.25
Eiffel Tower	300	– 196.5	38 612.25
Empire State	381	– 115.5	13 340.25
Petronas Towers	452	– 44.5	1 980.25
Taipei 101	509	+ 12.5	156.25
World Trade Centre	526	+ 29.5	870.25
CN Tower	553	+ 56.5	3 192.25
KVLY-TV Mast	629	+ 132.5	17 556.25
Warsaw Radio Mast	646	+ 149.5	22 350.25
Burj Khalifa	830	+ 333.5	111 222.25
	MEAN HEIGHT = 496.5 m		MEAN OF SQUARED DIFFERENCES = 22 597.525

Mean = 496.5 m
Variance = 22 597.525

Standard Deviation	= square root of variance
	= √ 22 597.525 = 150.32 m